Introducing the Rational Speech Act framework

Day 1: Language understanding as Bayesian inference

The Rational Speech Act (RSA) framework views communication as recursive reasoning between a speaker and a listener. The listener interprets the speaker’s utterance by reasoning about a cooperative speaker trying to inform a naive listener about some state of affairs. Using Bayesian inference, the listener infers what the state of the world is likely to be given that a speaker produced some utterance, knowing that the speaker is reasoning about how a listener is most likely to interpret that utterance. Thus, we have (at least) three levels of inference. At the top, the sophisticated, pragmatic listener, $L_{1}$ , reasons about the pragmatic speaker, $S_{1}$ , and infers the state of the world $s$ given that the speaker chose to produce the utterance $u$ . The speaker chooses $u$ by maximizing the probability that a naive, literal listener, $L_{0}$ , would correctly infer the state of the world $s$ given the literal meaning of $u$ .

At the base of this reasoning, the naive, literal listener $L_{0}$ interprets an utterance according to its meaning. That is, $L_{0}$ computes the probability of $s$ given $u$ according to the semantics of $u$ and the prior probability of $s$ . A standard view of the semantic content of an utterance suffices: a mapping from states of the world to truth values.

$P_{L_{0}}(s\mid u) \propto [\![u]\!](s) \cdot P(s)$

// possible states of the world
var worldPrior = function() {
  return uniformDraw([
    {shape: "square", color: "blue"},
    {shape: "circle", color: "blue"},
    {shape: "square", color: "green"}
  ])
}

// possible one-word utterances
var utterances = ["blue","green","square","circle"]

// meaning funtion to interpret the utterances
var meaning = function(utterance, world){
  return utterance == "blue" ? world.color == "blue" :
  utterance == "green" ? world.color == "green" :
  utterance == "circle" ? world.shape == "circle" :
  utterance == "square" ? world.shape == "square" :
  true
}

// literal listener
var literalListener = function(utterance){
  Infer({method:"enumerate"}, function(){
    var world = worldPrior();
    var uttTruthVal = meaning(utterance, world);
    condition(uttTruthVal == true)
    return world
  })
}

viz.table(literalListener("blue"))

Exercises:

Check what happens with the other utterances.

In the model above, worldPrior() returns a sample from a uniformDraw over the possible world states. What happens when the listener’s beliefs are not uniform over world states? (Hint, use a categorical distribution by calling categorical({ps: [list_of_probabilities], vs: [list_of_states]})).

Fantastic! We now have a way of integrating a listener’s prior beliefs about the world with the truth functional meaning of an utterance.

What about speakers? Speech acts are actions; thus, the speaker is modeled as a rational (Bayesian) actor. He chooses an action (e.g., an utterance) according to its utility. The speaker simulates taking an action, evaluates its utility, and chooses actions in proportion to their utility. This is called a softmax optimal agent; a fully optimal agent would choose the action with the highest utility all of the time. (This kind of model is called action as inverse planning; for more on this, see agentmodels.org.)

In the code box below you’ll see a generic softmax agent model. Note that in this model, agent uses factor (not condition). factor is a continuous (or, softer) version of condition that takes real numbers as arguments (instead of binary truth values). Higher numbers (here, utilities) upweight the probabilities of the actions associated with them.

// define possible actions
var actions = ['a1', 'a2', 'a3'];

// define some utilities for the actions
var utility = function(action){
  var table = { 
    a1: -1, 
    a2: 6, 
    a3: 8
  };
  return table[action];
};

// define speaker optimality
var alpha = 1

// define a rational agent who chooses actions 
// according to their expected utility
var agent = Infer({ method: 'enumerate' }, function(){
    var action = uniformDraw(actions);
    factor(alpha * utility(action));
    return action;
});

print("the probability that an agent will take various actions:")
viz.auto(agent);

Exercises:

Explore what happens when you change the agent’s optimality.

Explore what happens when you change the utilities.

In language understanding, the utility of an utterance is how well it communicates the state of the world $s$ to a listener. So, the speaker $S_{1}$ chooses utterances $u$ to communicate the state $s$ to the hypothesized literal listener $L_{0}$ . Another way to think about this: $S_{1}$ wants to minimize the effort $L_{0}$ would need to arrive at $s$ from $u$ , all while being efficient at communicating. $S_{1}$ thus seeks to minimize the surprisal of $s$ given $u$ for the literal listener $L_{0}$ , while bearing in mind the utterance cost, $C(u)$ . (This trade-off between efficacy and efficiency is not trivial: speakers could always use minimal ambiguity, but unambiguous utterances tend toward the unwieldy, and, very often, unnecessary. We will see this tension play out later in the course.)

Speakers act in accordance with the speaker’s utility function $U_{S_{1}}$ : utterances are more useful at communicating about some state as surprisal and utterance cost decrease.

$U_{S_{1}}(u; s) = log(L_{0}(s\mid u)) - C(u)$

(In WebPPL, $log(L_{0}(s\mid u))$ can be accessed via literalListener(u).score(s).)

With this utility function in mind, $S_{1}$ computes the probability of an utterance $u$ given some state $s$ in proportion to the speaker’s utility function $U_{S_{1}}$ . The term $\alpha > 0$ controls the speaker’s optimality, that is, the speaker’s rationality in choosing utterances.

$P_{S_{1}}(u\mid s) \propto exp(\alpha U_{S_{1}}(u; s))$

// pragmatic speaker
var speaker = function(world){
  Infer({method:"enumerate"}, function(){
    var utterance = utterancePrior();
    factor(alpha * literalListener(utterance).score(world))
    return utterance
  })
}

Exercise: Check the speaker’s behavior for a blue square.

We now have a model of the generative process of an utterance. With this in hand, we can imagine a listener who thinks about this kind of speaker.

The pragmatic listener $L_{1}$ computes the probability of a state $s$ given some utterance $u$ . By reasoning about the speaker $S_{1}$ , this probability is proportional to the probability that $S_{1}$ would choose to utter $u$ to communicate about the state $s$ , together with the prior probability of $s$ itself. In other words, to interpret an utterance, the pragmatic listener considers the process that generated the utterance in the first place. (Note that the listener model uses observe, which functions like factor with $\alpha$ set to $1$ .)

$P_{L_{1}}(s\mid u) \propto P_{S_{1}}(u\mid s) \cdot P(s)$

// pragmatic listener
var pragmaticListener = function(utterance){
  Infer({method:"enumerate"}, function(){
    var world = worldPrior();
    observe(speaker(world), utterance)
    return world
  })
}

Within the RSA framework, communication is thus modeled as in Fig. 1, where $L_{1}$ reasons about $S_{1}$ ’s reasoning about a hypothetical $L_{0}$ .

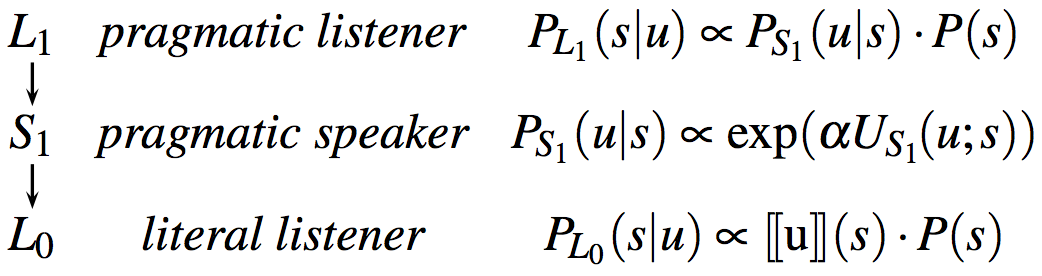
Fig. 1: Graphical representation of the Bayesian RSA model.

Fig. 1: Bayesian RSA schema.

Application 1: Simple referential communication

In its initial formulation, reft:frankgoodman2012 use the basic RSA framework to model referent choice in efficient communication. To see the mechanism at work, imagine a referential communication game with three objects, as in Fig. 2.

Fig. 2: Example referential communication scenario from Frank & Goodman (2012). Speakers choose a single word, $$u$$, to signal an object, $$s$$.

Fig. 2: Example referential communication scenario from Frank and Goodman. Speakers choose a single word, u, to signal an object, s.

Suppose a speaker wants to signal an object, but only has a single word with which to do so. Applying the RSA model schematized in Fig. 1 to the communication scenario in Fig. 2, the speaker $S_{1}$ chooses a word $u$ to best signal an object $s$ to a literal listener $L_{0}$ , who interprets $u$ in proportion to the prior probability of naming objects in the scenario (i.e., to an object’s salience, $P(s)$ ). The pragmatic listener $L_{1}$ reasons about the speaker’s reasoning, and interprets $u$ accordingly. By formalizing the contributions of salience and efficiency, the RSA framework provides an information-theoretic definition of informativeness in pragmatic inference.

// Here is the code from the Frank and Goodman RSA model

// possible states of the world
var worldPrior = function() {
  return uniformDraw([
    {shape: "square", color: "blue"},
    {shape: "circle", color: "blue"},
    {shape: "square", color: "green"}
  ])
}

// possible one-word utterances
var utterances = ["blue","green","square","circle"]

// meaning funtion to interpret the utterances
var meaning = function(utterance, world){
  return utterance == "blue" ? world.color == "blue" :
  utterance == "green" ? world.color == "green" :
  utterance == "circle" ? world.shape == "circle" :
  utterance == "square" ? world.shape == "square" :
  true
}


// literal listener
var literalListener = function(utterance){
  Infer({method:"enumerate"},
        function(){
    var world = worldPrior()
    condition(meaning(utterance, world))
    return world
  })
}

// set speaker optimality
var alpha = 1

// pragmatic speaker
var speaker = function(world){
  Infer({method:"enumerate"},
        function(){
    var utterance = uniformDraw(utterances)
    factor(alpha * literalListener(utterance).score(world))
    return utterance
  })
}

// pragmatic listener
var pragmaticListener = function(utterance){
  Infer({method:"enumerate"},
        function(){
    var world = worldPrior()
    observe(speaker(world),utterance)
    return world
  })
}

print("literal listener's interpretation of 'blue':")
viz.table(literalListener( "blue"))
print("speaker's utterance distribution for a blue circle:")
viz.table(speaker({shape:"circle", color: "blue"}))
print("pragmatic listener's interpretation of 'blue':")
viz.table(pragmaticListener("blue"))

Exercises:

Explore what happens if you make the speaker more optimal.

Add another object to the scenario.

Add a new multi-word utterance.

Check the behavior of the other possible utterances.

In the next chapter, we’ll see how RSA models have been developed to model more complex aspects of pragmatic reasoning and language understanding.

Table of Contents